Quick note on how the term “mode collapse” is overloaded when it comes to training neural networks.
If you’ve ever trained a VAE, then you’ve probably had to deal with VAE mode collapse. This is when no matter the input, it will output the same output which is roughly the average of your entire dataset.
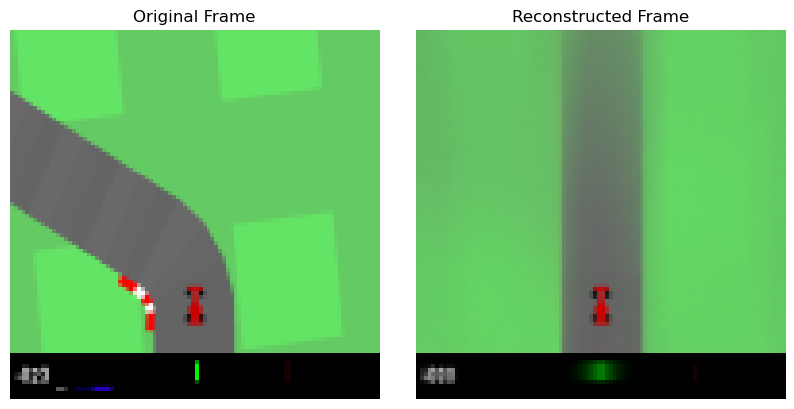
On the other hand, we also see mode collapse when training GANs, but this is an entirely different type of collapse. If you’re training your network to try and produce images of digits, producing an average is bad, but producing just the digit 1 or 7 counts as a strong generator. Rather than outputting the mean of all your data, GAN generators can learn to completely ignore certain classes of data while being indistinguishable from real input for the few classes it does learn.

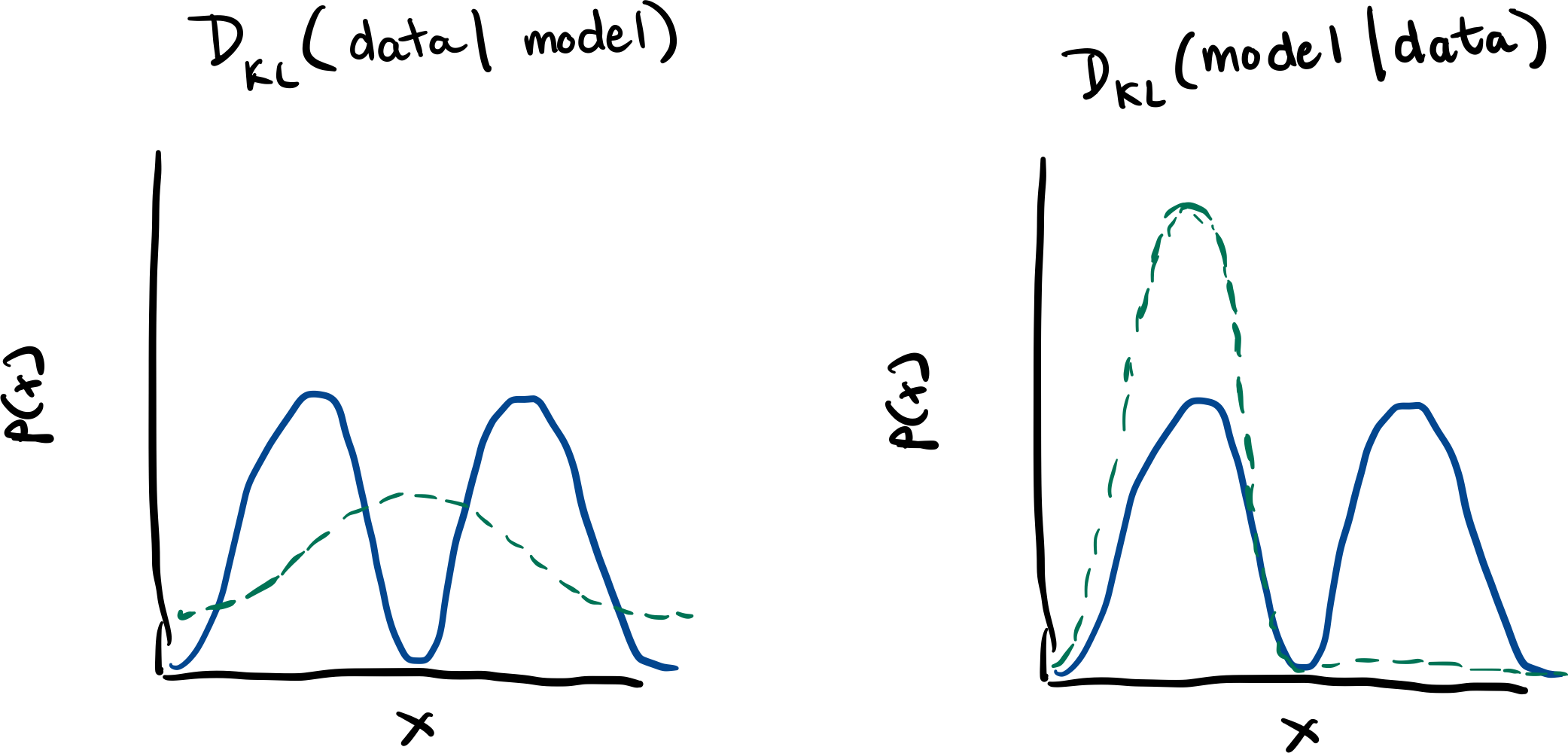 Here’s the rough model in my head for how these two
types of mode collapse differ. On the left, we have the
VAE loss which is trying to recreate the data given a
model (in our case, a latent variable). If our model is
too weak to represent the true distribution, the best it
can do is to average between the peaks. If our model
were to just model one of the peaks, the KL-Divergence
would become \infty.
Here’s the rough model in my head for how these two
types of mode collapse differ. On the left, we have the
VAE loss which is trying to recreate the data given a
model (in our case, a latent variable). If our model is
too weak to represent the true distribution, the best it
can do is to average between the peaks. If our model
were to just model one of the peaks, the KL-Divergence
would become \infty.
If we flip the KL-Divergence (creatively called Reverse KL), we’re trying to maximize the probability of the model given the data. Now dropping a mode is a valid solution doesn’t have the same behavior of boosting the divergence to \infty. Even though the KL-Divergence would be less if our model was able to capture both peaks, training dynamics of GANs lead to modeling less modes than the real distribution.
In one training, it collapses to the average of all your data and in the other, we drop certain modes.
- “It is now possible to train GANs using maximum likelihood, as described in section 3.2.4. These models still generate sharp samples, and still select a small number of modes. See figure 15.”
- GANs often choose to generate from very few modes; fewer than the limitation imposed by the model capacity. The reverse KL prefers to generate from as many modes of the data distribution as the model is able to; it does not prefer fewer modes in general. This suggests that the mode collapse is driven by a factor other than the choice of divergence.
Even if this intuition isn’t perfectly right for why GANs produce sharp images and drop modes (it might just be the training procedure we’re using), I think this still provides an intuitive image of how KL-Divergence differs when you flip which way it goes.